Representação algébrica para o padrão ou a regularidade de uma sequência

Definição¶

Uma sequência numérica é uma lista ordenada de números que seguem uma regra ou padrão.
Podemos usar a álgebra para descrever esse padrão por meio de uma expressão algébrica que relaciona a posição do termo na sequência (geralmente representada por $n$ ) com seu valor.

Justificativa¶

Neste ponto, observa-se que muitos estudantes têm dificuldades em identificar e generalizar padrões em sequências numéricas.
A simples observação dos termos não é suficiente: é fundamental que o aluno compreenda como a posição $n$ se relaciona com o valor de cada termo, desenvolvendo assim uma expressão algébrica que represente essa regularidade.

Essa habilidade é essencial para resolver problemas que envolvem regularidades, fórmulas e funções, favorecendo o raciocínio algébrico e a modelagem de situações matemáticas.

Verificar as regularidades¶

Neste passo, além dos operadores básicos e do operador % (módulo), utilizaremos o comando for da linguagem Julia para identificar ciclos e repetições, analisando padrões presentes em sequências numéricas.

Solução:¶

Problema 01¶

(Supletivo 2014). Na festa junina da escola, a professora de Artes resolveu fazer as bandeirinhas de São João conforme a sequência periódica de quatro cores. A cor da primeira bandeira é verde, a segunda é vermelha, a terceira é azul e a quarta é cinza. A partir daí, segue a sequência: verde, vermelho, azul, cinza, verde, vermelho, azul, cinza, e assim sucessivamente.

Qual é a cor da 55ª bandeira?

A) Verde B) Vermelho C) Azul D) Cinza

Solução:¶

As cores se repetem a cada quatro bandeiras. Logo, a cor de uma bandeira em uma determinada posição depende do resto da divisão dessa possição por 4. Assim, bandeiras de resto:

1 são verdes;
2 sao vermalhas;
3 são azuis e
0 sao cinzas

55%4

3

Portanto, a 55ª bandeira é azul.

Para resolver as questões de 02 a 05, utilizaremos o laço for para analisar cada alternativa e verificar as expressões apresentadas. O procedimento pode ser seguido nos seguintes passos:

Definir variáveis e expressões correspondentes aos termos da sequência;
Observar os padrões numéricos gerados por cada alternativa;
Comparar e representar os padrões por meio das expressões algébricas indicadas nas alternativas;
Testar e validar qual alternativa corresponde corretamente à sequência.

Problema 02¶

(Supletivo 2010)

Observe a quantidade de figuras em cada coluna no quadro abaixo:

Coluna 1	Coluna 2	Coluna 3	Coluna 4	$\cdots$
🙂🙂🙂	🙂🙂🙂	🙂🙂🙂	🙂🙂🙂
	🙂🙂🙂	🙂🙂🙂	🙂🙂🙂	$\cdots$
		🙂🙂🙂	🙂🙂🙂
			🙂🙂🙂

Mantendo esse mesmo padrão, a expressão algébrica que representa o número de figuras $(F)$ na ordem $n$ $(n = 1, 2, 3, \cdots)$ é:

A) $F(n) = 3n + 1$
B) $F(n) = 3n$
C) $F(n) = 2n + 1$
D) $F(n) = 4n - 1$

Solução:¶

for n in 1:5
    println("$n → ",3n) 
end

Problema 03¶

(Prova Brasil).
As variáveis $n$ e $P$ assumem valores conforme mostra o quadro abaixo:

n	5	6	7	8	9	10
P	8	10	12	14	16	18

A relação entre $P$ e $n$ é dada pela expressão:

A) $P = n + 1$
B) $P = n + 2$
C) $P = 2n - 2$
D) $P = n - 2$

Solução:¶

for n in 5:10
    println("$n → ",2n-2) 
end

Problema 04¶

(SAEPE)

Observe a sequência numérica abaixo:

$n$	1	2	3	4	5	$\cdots$
$a_n$	0	3	8	15	24	$\cdots$

A expressão algébrica que permite calcular o enésimo termo dessa sequência ( $a_n$ ) em função da posição $n$ é:

A) $2n - 1$
B) $2n + 2$
C) $n^2 - 1$
D) $n^2 + 2$

Solução:¶

for n in 1:5
    println("$n → ",n^2 - 1) 
end

Problema 05¶

(P. Wr)

As figuras mostradas abaixo estão organizadas dentro de um padrão que se repete:

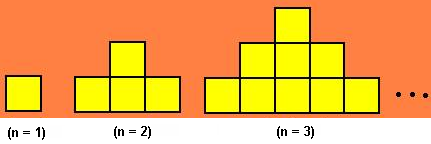
Mantendo essa disposição, a expressão algébrica que representa o número de quadradinhos $Q$ em função da ordem $n$ ( $n = 1, 2, 3, \dots$ ) é:

A) $Q = n$
B) $Q = n^2$
C) $Q = n^2 + 1$
D) $Q = n^2 + 2$

Solução:¶

for n in 1:5
    println("$n → ",n^2) 
end

Matematica.jl

Valor numérico de uma expressão algébrica

Matematica.jl

Calculadora de Frações