Máximos e mínimos locais de funções de duas variáveis¶
A modelagem matemática de fenômenos físicos (em áreas como Mecânica Clássica, Termodinâmica, Óptica, etc.), de processos da Engenharia e Economia - entre outras atividades de grande relevância para o empreendimento humano - naturalmente recai sobre o estudo de funções de múltiplas variáveis, uma vez que estes lidam com intricados fatores que interagem entre si e dependem uns dos outros. Em particular, funções de duas variáveis aparecem com bastante frequência nos exemplos citados.
Considere, por exemplo, a modelagem do lucro de uma empresa dado em função do preço dos seus dois principais produtos, . Encontrar os valores de e que maximizariam o lucro é um problema clássico do Cálculo Diferencial e Integral, que envolve determinar os chamados pontos de máximo e mínimo locais da função .
Munidos das ferramentas do Cálculo, o Teorema Espectral nos permite uma análise do problema sob a ótica da Álgebra Linear, o que por muitas vezes oferece uma solução mais prática.
A ideia central é analisarmos as propriedades da matriz Hessiana, uma das principais ferramentas do Cálculo Vetorial, que é constituída das derivadas parciais de segunda ordem da função, que naturalmente nos fornecem informações sobre os pontos de máximo e mínimo, chamados pontos críticos.
Para o caso em que as derivadas de segunda ordem são contínuas, tem-se que . Logo, a matriz Hessiana é simétrica e sabemos, pelo Teorema Espectral, que possuirá autovalores reais. Em suma, isto nos permite classificar os pontos críticos com base nos seus autovalores.
Similarmente à estratégia usual do Cálculo, inicialmente devemos encontrar pontos que são candidatos a máximos, mínimos ou pontos de sela. Tais pontos satisfazem o seguinte sistema:
onde é o gradiente de , outro elemento protagonista do Cálculo Vetorial, que basicamente consiste do vetor cujas coordenadas são as derivadas de em cada variável respectiva.
A partir daí, calculamos a matriz Hessiana para os pontos encontrados e encontramos seus autovalores. A natureza do ponto crítico é então determinada pelos sinais dos seus autovalores, e :
- Mínimo local: e (a Hessiana é definida positiva);
- Máximo local: e (a Hessiana é definida negativa);
- Ponto de sela: (a Hessiana é indefinida);
Para o caso em que algum autovalor for zero, o teste é inconclusivo. É necessária análise de derivadas de ordem superior.
Assim, a forma diagonal da matriz Hessiana nos revela a curvatura da função nas direções dos autovetores. Por exemplo, se e a função tem concavidade para cima em todas as direções.
Tomemos um exemplo prático: Considere . Utilizando (2) encontramos o ponto crítico , cuja Hessiana é dada por , já diagonal. Encontramos que seus autovalores são e , resultando na conclusão que é um mínimo local.
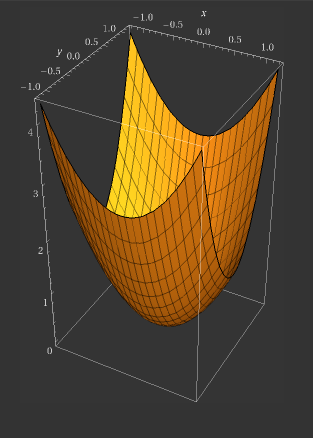
Figure 1:Gráfico 3D da função
Trazendo para um cenário análogo ao exemplo da função de lucro discutida no início, se tal corresponde a um custo dependente dos parâmetros , sabemos que tomando-os estaríamos minimizando o custo.