Contextualização¶
Um dos principais exemplos de como matrizes podem ser aplicadas no meio computacional é o processamento de imagens. Em geral, a maioria dos softwares lidam com imagens tratando-as como uma matriz de pixels (à nível de manipulação e processamento, já o armazenamento em disco é feito utilizando outros formatos mais eficientes, como os conhecidos formatos .JPG, .PNG, entre outros), com dimensões correspondentes as da resolução da imagem.
Um pixel é a unidade fundamental que compõe uma imagem, ele é basicamente uma cor sólida. A composição de milhares de pixels (por exemplo, uma imagem de resolução 800 x 600 contém pixels) resulta na imagem como a enxergamos. A cor de um pixel é armazenada como um conjunto de números, que representam as escalas de cada espectro principal de cor e luz, que unidos formam a cor desejada - logo, na verdade uma imagem é uma matriz tridimensional, pois cada pixel que a compõe armazena mais de um valor.
O RGB é um dos sistemas de cores mais conhecidos e utilizados, cuja sigla vem do inglês Red (Vermelho), Green (Verde) e Blue (Azul), uma vez que todas as outras cores (ou pelo menos a maioria) podem ser obtidas através da adição dessas três. No padrão RGB, cada pixel contém valores entre 0 e 255 para cada uma das três cores base, representando as suas respectivas intensidades. Por exemplo, um pixel contendo os valores (255, 0, 0) - para vermelho, verde e azul, respectivamente - terá cor vermelha sólida, enquanto um com (255, 255, 0) terá cor amarela (vermelho mais verde), (0, 0, 0) terá cor preta e (255, 255, 255) terá cor branca. Então, na representação matricial de uma imagem de resolução no formato RGB, o que teremos serão 3 matrizes de dimensão , uma para cada uma das cores base, com as entradas variando de 0 a 255.
Como vimos no Teorema de Eckart-Young, é possível aproximar uma matriz por outra de mesma dimensão e posto menor, descartando (anulando) os valores singulares de índice maior ao do posto escolhido, na sua decomposição SVD. Então, quais seriam os efeitos de aplicar essa técnica às matrizes RGB de uma imagem? Acontece que, na verdade, esse é um método de compressão de imagens válido, que é aplicado em algumas situações no meio digital.
O conceito de comprimir uma imagem consiste em reduzir o seu tamanho (a quantidade de informações que ela armazena, o que é refletido no espaço que ela ocupa em disco), de maneira que não haja uma perda significativa na sua qualidade. Existem diversos métodos de compressão de imagens, cada um com propósitos diferentes, e a compressão via SVD truncada é um deles. Em geral, é mais utilizado quando lida-se com imagens de complexidade menor, onde a estrutura global é mais importante (muito comum no contexto de Visão Computacional), tendo como vantagem um controle maior do nível de compressão, definido diretamente pelo posto para o qual serão aproximadas as matrizes originais.
Nesse tópico, mostraremos uma implementação (relativamente simples) desse método de compressão na linguagem Python, fazendo uso dos conceitos vistos no tópico de Valores Singulares e recursos oferecidos por bibliotecas da linguagem Python. Analisaremos os efeitos da compressão em uma imagem de teste, considerando valores diferentes para o posto de aproximação.
O Algoritmo¶
A ideia geral para o algoritmo provém do que discutimos até agora:
Receber uma imagem e “quebrá-la” nas 3 matrizes RGB correspondentes;
Decompor em valores singulares cada uma das 3 matrizes;
Fazer a redução do posto para cada uma delas;
Reconstruir a imagem a partir das novas matrizes aproximadas.
Felizmente, as bibliotecas Numpy e PIL do Python fornecem implementações dos principais recursos que precisaremos. Aqui está a implementação do algoritmo:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44from PIL import Image import numpy as np # Abre uma imagem e extrai as matrizes R, G, B imagem_original = Image.open("original.jpg") matriz_original = np.array(imagem_original) matriz_r = matriz_original[:, :, 0] matriz_g = matriz_original[:, :, 1] matriz_b = matriz_original[:, :, 2] # Decompõe as matrizes RGB em valores singulares Ur, Sr, Vrt = np.linalg.svd(matriz_r) Ug, Sg, Vgt = np.linalg.svd(matriz_g) Ub, Sb, Vbt = np.linalg.svd(matriz_b) k = 100 #posto escolhido # Trunca as matrizes SVD do RGB para o posto k Ukr = Ur[:, :k] # Todas as linhas, primeiras k colunas Skr = Sr[:k] # Primeiros k elementos Vtkr = Vrt[:k, :] # Primeiras k linhas, todas as colunas Ukg = Ug[:, :k] Skg = Sg[:k] Vtkg = Vgt[:k, :] Ukb = Ub[:, :k] Skb = Sb[:k] Vtkb = Vbt[:k, :] # Reconstrói as matrizes RGB a partir da forma SVD truncada R_approx = Ukr @ np.diag(Skr) @ Vtkr G_approx = Ukg @ np.diag(Skg) @ Vtkg B_approx = Ukb @ np.diag(Skb) @ Vtkb # Garante que as entradas das novas matrizes estejam entre 0 e 255 R_approx = np.clip(R_approx, 0, 255).astype(np.uint8) G_approx = np.clip(G_approx, 0, 255).astype(np.uint8) B_approx = np.clip(B_approx, 0, 255).astype(np.uint8) # Reconstrói a imagem a partir das novas matrizes RGB imagem_reconstruida = np.stack((R_approx, G_approx, B_approx), axis=-1).astype(np.uint8) Image.fromarray(imagem_reconstruida).save("reconstruida.jpg")
Algoritmo de compressão de imagem via SVD truncada
Observe que a decomposição SVD é realizada pelo método linalg.svd, da biblioteca Numpy, que retorna as matrizes , um vetor S contendo os valores singulares ordenados (ou seja, a diagonal principal da matriz e não ela própria. Inclui também os valores singulares nulos) e , respectivamente. As funções do módulo Image da biblioteca PIL nos permitem realizar as conversões entre imagem e matriz (que é um array multidimensional).
A separação das matrizes RGB e o truncamento são realizados aproveitando-se do poderoso recurso de slicing (fatiamento) de arrays do Python (a sintaxe “[: : :]”). No caso dos arrays U, S e Vt, o que obtemos é o seguinte:
U (originalmente uma matriz ) é truncado nas primeiras colunas, obtendo uma nova matriz ;
S (originalmente um vetor de dimensão igual ao ) é truncado nos primeiros elementos, obtendo um vetor de dimensão (contendo os valores singulares );
Vt (originalmente uma matriz ) é truncado nas primeiras linhas, obtendo uma nova matriz .
Esse processo de truncamento é equivalente a considerar os valores singulares de índice maior que na matriz iguais a zero, conforme descrito na definição da matriz e no Teorema de Eckart-Young.
Logo, as matrizes RGB aproximadas, obtidas nos produtos entre suas respectivas matrizes SVD truncadas (realizado no python com o operador “@”, de produto matricial. O método np.diag é utilizado para transformar o vetor truncado Sk na matriz diagonal truncada ), preservam a dimensão de das matrizes originais (). Isso implica que a imagem final comprimida terá resolução (dimensão) igual a da imagem original, logo, o processo realiza uma redução de complexidade da imagem, e não uma redução de resolução (este último que é comum em outros métodos que visam reduzir o tamanho de uma imagem).
O uso da função np.clip, nas linhas 38-40, é importante para garantir que as entradas das matrizes resultantes dos produtos estejam no intervalo permitido pelo padrão RGB, entre 0 e 255. A função substitui por 0 entradas com valor abaixo de 0, assim como por 255 entradas acima de 255, preservando as que estão dentro do intervalo. A presença de entradas fora desse intervalo resultaria em pixels “defeituosos” no resultado final, com cores destoantes da imagem original.
Testes e resultados¶
Agora, veremos os resultados obtidos aplicando o algoritmo em uma imagem de testes, para diferentes valores de . Note que o valor escolhido no algoritmo é livre, não há um controle sobre o valor escolhido em relação ao posto das matrizes originais. Mas, se escolhermos maior que o posto, na prática não ocorrerá alteração alguma na imagem.
Utilizaremos uma imagem de alta resolução (6000 x 4000) e iremos variar para os valores 10, 50, 150, 500 e 1000. A nossa métrica para a compressão será o espaço em disco ocupado pelas imagens, com a imagem original possuindo 7,4 MB (Megabytes), e determinaremos o percentual de compressão pela seguinte fórmula:
Vejamos os resultados:

Imagem original. Tamanho: 7,4MB

Imagem comprimida com = 10. Tamanho: 1,2MB (Compressão de 83,78%).

Imagem comprimida com = 50. Tamanho: 1,8MB (Compressão de 75,67%).

Imagem comprimida com = 150. Tamanho: 2,4MB (Compressão de 67,56%).

Imagem comprimida com = 500. Tamanho: 2,8MB (Compressão de 62,16%).

Imagem comprimida com = 1000. Tamanho: 3,0MB (Compressão de 59,45%).
Note como de = 10 para = 50 a imagem se torna completamente distinguível. Como mencionado no início do tópico, para aplicações em áreas como Visão Computacional esse tipo de compressão é bastante vantajoso, veja como no caso = 50 tivemos uma compressão de mais de 75%, preservando consideravelmente a estrutura e os detalhes principais da imagem.
O mais interessante é que a partir de = 500, a imagem já parece quase idêntica a original (ao menos a olho nu), com = 1000 apenas aumentando a nitidez de alguns detalhes (abrindo as imagens em tela cheia é possível perceber melhor). Ao final, temos uma imagem extremamente próxima a original, com o tamanho reduzido em quase 60%.
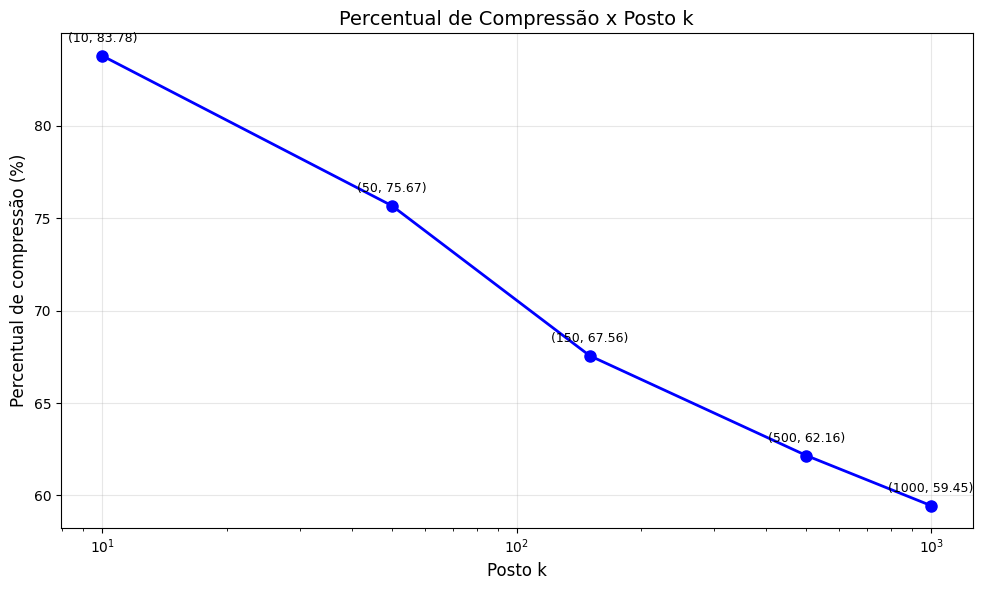
Gráfico com os resultados obtidos.
Também é possível, a partir da decomposição SVD da imagem original, extrair seus valores singulares e componentes correspondentes, para uma análise mais geral do comportamento da compressão para diferentes valores de . Visualizando essas informações, podemos identificar a partir de qual componente os valores singulares se anulam (no caso que a matriz não possui posto completo), se aproximam de zero ou passam a variar pouco, sendo então essa componente uma possível escolha para .
Fazendo isso para as matrizes RGB, podemos identificar a contribuição de cada canal na imagem, possibilitando escolher um específico para cada um. Imagens com cores predominantemente verdes, por exemplo, terão o canal verde com maiores valores singulares. Isso fica evidente na imagem de testes:
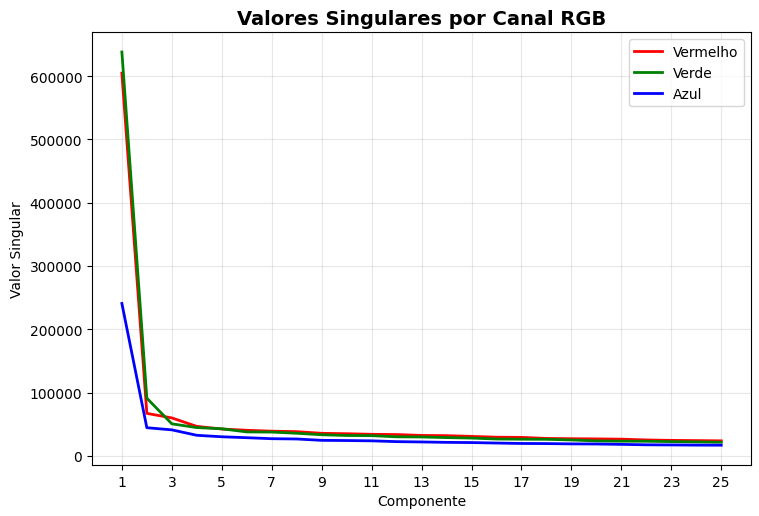
Valores singulares e componentens correspondentes das matrizes de cada canal RGB.
Percebemos que os maiores valores singulares estão concentrados nas primeiras componentes, e que a partir da componente 5 os valores já estão estáveis, passando a decrescer suavemente. Os primeiros valores, maiores, carregam as informações mais gerais da imagem, como seu formato e silhueta, enquanto que os valores seguintes são responsáveis por detalhes mais finos, como nitidez e textura. Isso se alinha com o fato de que, ao fazermos , a imagem resultante preserva um aspecto geral da imagem original, sua silhueta. A falta de nitidez, nesse caso, se deve à perda dos valores singulares restantes que, em especial nessa imagem (que tem dimensão grande), são muitos.
Como os valores singulares são grandes, a escala logarítmica proporciona uma visualização mais ampla. Podemos ainda, converter a imagem para a escala de cinza, que resulta em um único canal de cor (e consequentemente uma única matriz para analisarmos):
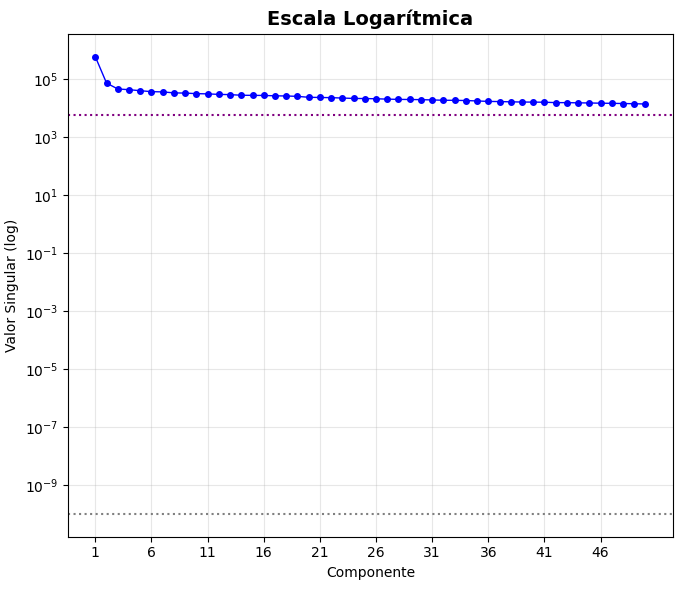
Valores singulares (em escala logarítmica) e componentes correspondentes da matriz da imagem em escala de cinza.
Em particular, note que os valores singulares nunca se anulam, logo a matriz tem posto completo. De certa forma, esse é o caso mais complicado para se escolher , pois se não tivesse posto completo uma escolha clara para seria a última componente não nula (ou não muito próxima de zero).
Alinhadas a esses dados, as imagens resultantes dos valores de testados nos indicam que a partir da componente 1000, aproximadamente, devemos ter uma variação muito baixa dos valores singulares, uma vez que a diferença de qualidade se torna praticamente imperceptível.